La radice di due: il numero che spezzò l’armonia
C’è un numero che non nasce da un calcolo complicato, ma da un gesto elementare: tracciare una diagonale.
Basta disegnare un quadrato di lato uno e unire due vertici opposti. La lunghezza di quel segmento è √2. Nulla di più semplice, nulla di più destabilizzante.
Tra i numeri che abitano la matematica, pochi hanno avuto un destino così perturbante come questo. √2 non è un numero grande, non è difficile da definire, eppure ha incrinato una delle convinzioni più antiche e potenti del pensiero umano: che tutto ciò che esiste possa essere ricondotto a un rapporto tra numeri interi.
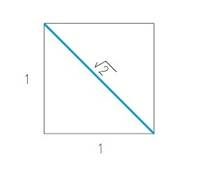
Un numero che nasce da un gesto semplice
Per molto tempo si credette che ogni lunghezza potesse essere detta come frazione. Era un’idea potente, quasi morale: il mondo è ordinato perché è numerabile. Questa convinzione, attribuita alla scuola di Pitagora, non distingueva tra matematica, musica e cosmo. Tutto era proporzione.
Poi arrivò √2.
Scoprire che la diagonale del quadrato non è commensurabile con il lato significò scoprire che esistono grandezze reali che sfuggono al linguaggio delle frazioni. Non era un dettaglio tecnico: era una crepa nella visione del mondo.
La tradizione racconta che chi rivelò questa verità fu punito per aver infranto un segreto sacro. Che la leggenda sia vera o no, coglie un punto essenziale: √2 non è soltanto un numero, è una frattura filosofica.
L’irrazionale come scandalo
√2 è il primo numero irrazionale riconosciuto nella storia. “Irrazionale” non nel senso di caotico, ma nel suo significato originario: non dicibile come rapporto.
Per i pitagorici, il mondo era armonia numerica. La musica, l’astronomia, persino l’etica erano governate da proporzioni semplici. √2 dimostrava che esistono lunghezze reali che sfuggono a questa armonia.
Non sorprende che gli Elementi di Euclide, nel Libro X, dedichino un’attenzione quasi ossessiva alla classificazione delle grandezze incommensurabili, come se la matematica, ferita, cercasse di ricucire se stessa attraverso il rigore.
Qui la matematica incontra la filosofia. Platone suggerisce che il mondo sensibile partecipa delle idee senza mai esaurirle completamente. √2 sembra darne una traduzione numerica: nasce da una figura perfetta, il quadrato, ma non si lascia chiudere in una formula finita.
Un numero esatto e infinito
√2 è perfettamente definito. Non è approssimazione, non è incertezza. Eppure la sua scrittura decimale non termina mai, non si ripete, non concede tregua.
È un numero esatto che si manifesta come infinito.
Questa doppia natura lo rende sorprendentemente vicino a certe immagini letterarie. Ogni tentativo di spiegare il mondo, scrive Borges, produce nuove zone d’ombra. √2 non oscura la realtà: ne mostra l’abbondanza.
Non tutto ciò che è vero è comprimibile.
Non tutto ciò che è rigoroso è semplice.
Dal trauma all’eleganza: √2 diventa forma
Col tempo, l’irrazionale smette di essere un nemico. La matematica impara a conviverci e persino a usarlo come principio di ordine. Accade allora qualcosa di sorprendente: √2 entra nella vita quotidiana.
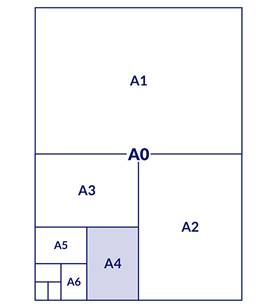
I formati dei fogli della serie A – A0, A1, A2, A3, A4 – sono costruiti in modo tale che il rapporto tra il lato lungo e quello corto sia sempre √2. Ogni piega produce un rettangolo simile al precedente. Nessuna perdita di forma, nessuna distorsione.
Non è un dettaglio tecnico, ma un’idea matematica incarnata nella materia. Ogni volta che pieghiamo un foglio o stampiamo una pagina A4, stiamo maneggiando un irrazionale addomesticato, reso utile, quotidiano.
Il numero che insegna un limite
√2 è il primo numero che insegna alla matematica un limite, ma non come sconfitta. È un limite generativo. Mostra che esiste sempre uno scarto tra modello e realtà, tra figura e misura.
In questo senso, √2 È una metafora dell’esperienza umana: ogni tentativo di comprendere il mondo produce qualcosa che eccede le nostre categorie. Ed è proprio lì che inizia la conoscenza più profonda.
La radice di due non è un numero ribelle. È un numero onesto.
Lascia un commento